Background
The Poisson Multi-Bernoulli Mixture (PMBM) filter is a gold standard for multi-target tracking. It is a sophisticated variation of Multiple Hypothesis Tracking (MHT), where the probabilities of all sufficiently plausible data association hypotheses are calculated. For each of the data association hypotheses in the prior distribution, there will be several new association hypotheses in the posterior distribution. This differs from tracking methods such as Joint Probabilistic Data Association (JPDA) where the data association hypotheses are combined after every estimation cycle in order to mitigate complexity.
This leads to an exponential growth in the number of hypotheses, which typically is mitigated by pruning low-probability hypotheses. Unfortunately, it will inevitably happen sooner or later that the true hypothesis is among those that are pruned. To mitigate the impact of this it is desirable to maintain individual track components, even if they fail to be supported by any hypothesis. To achieve this, we have to calculate the marginal probability that a given track component corresponds to a real target.
In the context of the JPDA, techniques have been developed for calculating such marginal probabilities without explicit hypothesis enumeration. It is possible to evaluate these exactly by formulating the problem as marginalisation in a factor graph. A more popular alternative is Loopy Belief Propagation (LBP), which also builds upon a factor graph formulation, but is more straightforward to implement due to its approximative nature.
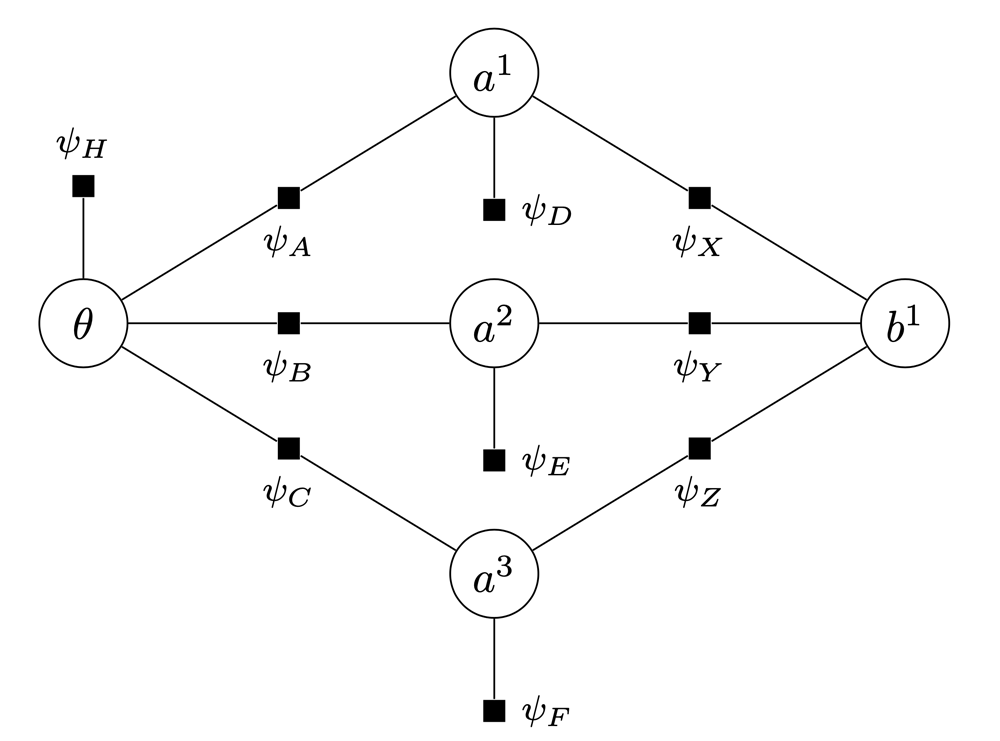 |
| Factor graph for an example with two prior hypotheses, three Bernoulli components and one measurement. |
Scope
The purpose of this project is to investigate whether exact and approximative factor graph techniques (e.g., Bayes tree and LBP) can be used to calculate marginal association probabilities in MHT/PMBM. The main challenge, and difference from the use of similar techniques in JPDA, is that the solution now must include marginalisation over several prior association hypotheses, instead of just a single prior association hypothesis.
Proposed Tasks for the 5th year project
The following tasks are proposed for the specialisation project:
- Make yourself familiar with MHT, PMBM and existing implementations that you can build upon.
- Make yourself familiar with factor graphs, Bayes tree and belief propagation.
- Formulate a factor graph model for marginal track probabilities in multi-hypothesis tracking.
- Implement a Bayes tree solution for simple toy examples.
- Implement an LBP solution for simple toy examples.
- Compare Bayes tree and LBP with brute force hypothesis enumeration.
- Write report.
Proposed Tasks for the master thesis
In the MSc thesis the goal will be to scale up the results from toy examples to realistic tracking problems, and to integrate the techniques in a complete PMBM-based tracking system. Possible code bases that this can build upon include (Brekke and Tokle 2022) and (Garcia-Fernandez et al. 2018). Ideally, this could be a collaboration with the project The PMBM filter 1 - The world’s most powerful tracker.
 |
| Example where marginal track probabilities could be useful: At the middle time step the misdetection hypothesis for the yellow target fails to get support from any of the association hypotheses, leading to premature track termination. |
Prerequisites
The candidate should have had the course TTK4250 Sensor Fusion, or exposure to probabilistic graphical models through other courses.
References
Williams, J. and Lau, R. (2014). “Approximate evaluation of marginal association probabilities with belief propagation.” IEEE Transactions on Aerospace and Electronic Systems, vol. 50, no. 4.
Williams, J. (2015). “Marginal multi-Bernoulli filters: RFS derivation of MHT, JIPDA, and association-based member.” IEEE Transactions on Aerospace and Electronic Systems, vol. 51, no. 3.
Garcia-Fernandez, A., Williams, J., Granström, K and Svensson, L. (2018). “Poisson multi-Bernoulli mixture filter: direct derivation and implementation.” IEEE Transactions on Aerospace and Electronic Systems.
Contact
Supervisor: Edmund Brekke.